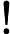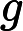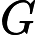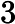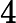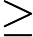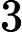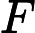首先正难则反，先算不存在的方案数再用 \(n!\) 减去。
考虑这个排列的析合树。
若根为合点，则儿子序列上的任何连续子序列都将是一个连续段。
故此时条件等价于第一个儿子和最后一个儿子的大小都不小于 \(n-k\)。
考虑设 \(g_i\) 表示长度为 \(i\) 且满足任意前缀都不是包含 \(1\) 的连续段的排列个数。
这样的排列可以作为其中一个儿子。
有递推式 \(g_i = i! - \sum\limits_{j=1}^{i-1} g_j (i-j)!\)。
此部分复杂度为 \(O(n^2)\)。
枚举第一个和最后一个儿子的大小，从而这种情况的答案为 \[ 2\sum\limits_{i=n-k}^k \sum\limits_{j=n-k}^{n-i} g_i g_j (n-i-j)! \]
这可以直接 \(O(n^2)\) 枚举计算。
若根为析点，则只需要保证每个儿子的大小不超过 \(k\) 即可。
设 \(f_i\) 表示长度为 \(i\) 的不存在非平凡连续段的排列个数。
这样的排列可以作为根的儿子序列，而儿子内部可以任意排列。
考虑递推 \(f_i\)。
可以用所有方案减去根为合点的方案再减去根为析点但儿子个数不超过 \(i-1\) 的方案。
其中有初值 \(f_1=1,f_2=2\)。
设 \(G_{i,j}\) 表示将 \(i\) 个数划分为 \(j\) 个排列的方案数。这可以简单地 \(O(n^3)\) 递推得到。
则有递推式 \[
f_i = i! - 2\sum\limits_{j=1}^{i-1} g_j (i-j)! - \sum\limits_{j=4}^{i-1} f_j G_{i,j} \qquad (i\ge 3)
\]
求得 \(f\) 后，考虑类似地设 \(F_{i,j}\) 表示将 \(i\) 个数划分为 \(j\) 个大小不超过 \(k\) 的排列的方案数，同样可以简单递推得到。
于是这种情况的答案为 \[
\sum\limits_{i=4}^n f_i F_{n,i}
\]
综上，总答案为 \[ n! - 2\sum\limits_{i=n-k}^k \sum\limits_{j=n-k}^{n-i} g_i g_j (n-i-j)! - \sum\limits_{i=4}^n f_i F_{n,i} \]
复杂度 \(O(n^3)\)，虽然这个瓶颈实际上看起来非常不优美，但是出题人并不想让一道看起来比较健康的签到题变成毒瘤题（或者说原题）。
代码： 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
using namespace std;
const int N = 400;
const int mod = 1e9 + 7;
int n,k;
int fac[N + 5];
int f[N + 5],g[N + 5];
int F[N + 5][N + 5],G[N + 5][N + 5];
int ans;
int main()
{
scanf("%d%d",&n,&k),fac[0] = 1;
for(register int i = 1;i <= n;++i)
fac[i] = (long long)fac[i - 1] * i % mod;
for(register int i = 1;i <= n;++i)
{
g[i] = fac[i];
for(register int j = 1;j < i;++j)
g[i] = (g[i] - (long long)g[j] * fac[i - j] % mod + mod) % mod;
}
G[0][0] = 1;
for(register int i = 1;i <= n;++i)
for(register int j = 1;j <= i;++j)
for(register int x = 1;x <= i;++x)
G[i][j] = (G[i][j] + (long long)G[i - x][j - 1] * fac[x]) % mod;
f[1] = 1,f[2] = 2;
for(register int i = 3;i <= n;++i)
{
f[i] = fac[i];
for(register int j = 1;j < i;++j)
f[i] = (f[i] - 2LL * g[j] * fac[i - j] % mod + mod) % mod;
for(register int j = 4;j < i;++j)
f[i] = (f[i] - (long long)f[j] * G[i][j] % mod + mod) % mod;
}
F[0][0] = 1;
for(register int i = 1;i <= n;++i)
for(register int j = 1;j <= i;++j)
for(register int x = 1;x <= min(i,k);++x)
F[i][j] = (F[i][j] + (long long)F[i - x][j - 1] * fac[x]) % mod;
for(register int i = n - k;i <= k;++i)
for(register int j = n - k;j <= n - i;++j)
ans = (ans + 2LL * g[i] * g[j] % mod * fac[n - i - j]) % mod;
for(register int i = 4;i <= n;++i)
ans = (ans + (long long)f[i] * F[n][i]) % mod;
ans = (fac[n] - ans + mod) % mod;
printf("%d\n",ans);
}