假设把原串放在后缀树上,LCP 即后缀树上的 LCA。
看看题目里这个式子,不觉得……很像树上路径长度?
所以可以对于每条边,算它的贡献。
DP 即可。
考虑一条边的贡献。
其实就是 ,又是熟悉的式子。
然后要知道一个性质,后缀树相当于把原串翻转之后插进后缀自动机后的 Parent Tree。
代码:
1 |
|
假设把原串放在后缀树上,LCP 即后缀树上的 LCA。
看看题目里这个式子,不觉得……很像树上路径长度?
所以可以对于每条边,算它的贡献。
DP 即可。
考虑一条边的贡献。
其实就是 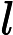
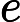

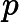

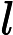
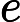

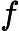
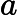
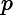
然后要知道一个性质,后缀树相当于把原串翻转之后插进后缀自动机后的 Parent Tree。
代码:
1 | #include <cstdio> |
Related Issues not found
Please contact @Alpha1022 to initialize the comment