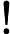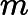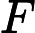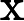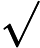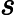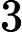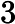LibreOJ 6609 无意识的石子堆 加强版

类似中国象棋，对于一个这样的二分图我们往往考察其每个连通块的构造。
分别用 x,y 计量左右部点的个数，两维均是 EGF。

一个连通块有三种情况：环、链、点，接下来我们分别来考虑它们。

对于环，它显然是偶环，那么左右部点的个数是一样的，并且正反各会被统计一次。而一边是排列，另一边是环排列，因此就是 12(−ln(1−xy)−xy)

对于链，右部点一定比左部点多一个，并且正反各会被统计一次。且两边都是排列，因此 12xy21−xy

对于点，必然是一个右部点，因此 y

现在将它们组合，那么答案就是 n!m![xnym]F(x,y)=n!m![xnym]exp(12(−ln(1−xy)−xy)+12xy21−xy+y)=n!m![sntm−n]exp(12(−ln(1−s)−s)+12st1−s+t)=n!m![sntm−n]exp(12(−ln(1−s)−s))et∑k≥01k!(12st1−s)k=n!mn_[sn]exp(12(−ln(1−s)−s))∑k≥0(m−nk)(12s1−s)k=n!mn_[sn]exp(12(−ln(1−s)−s))(1+12s1−s)m−n=n!mn_[sn]1√1−se−s/2(2−s2−2s)m−n

而其三者均微分有限，故其乘积也微分有限，借助计算机便可得到递推式 fn=12n((m−2n−3)fn−1+(3−n)fn−2−12fn−3)

代码：

#include <cstdio>
using namespace std;
const int N = 2e6;
const int mod = 943718401;
inline int fpow(int a,int b)
{
    int ret = 1;
    for(;b;b >>= 1)
        (b & 1) && (ret = (long long)ret * a % mod),a = (long long)a * a % mod;
    return ret;
}
int n,k;
long long m;
int f[N + 5],ans;
int main()
{
    scanf("%d%lld",&n,&m),k = (m - n) % mod;
    f[0] = 1,
    f[1] = 471859201LL * k % mod,
    f[2] = (825753601LL * k % mod * k + 589824001LL * k + 707788801) % mod * 2 % mod,
    f[3] = (924057601LL * k % mod * k % mod * k + 766771201LL * k % mod * k + 550502401LL * k + 786432001) % mod * 6 % mod;
    for(register int i = 4;i <= n;++i)
        f[i] = (k + 3LL * (i - 1)) * f[i - 1] % mod,
        f[i] = (f[i] + (3LL - i + mod) * (i - 1) % mod * f[i - 2]) % mod,
        f[i] = (f[i] + 471859200LL * (i - 1) % mod * (i - 2) % mod * f[i - 3]) % mod,
        f[i] = 471859201LL * f[i] % mod;
    ans = 1;
    for(register int i = 1;i <= n;++i)
        ans = (m - i + 1) % mod * ans % mod;
    ans = (long long)ans * f[n] % mod;
    printf("%d\n",ans);
}